台大机器学习2017课程笔记-回归

回归：输出为数值

• 股票市场预测=>道琼斯指数
• 自动驾驶汽车=>方向盘角度
• 推荐系统=>购买可能性

线性回归

模型

$$y = b + wx$$

损失函数

$$L(f) = \sum_{i=1}^{n}(\hat{y}^i-f(x^i))^2$$ $$L(w,b) = \sum_{i=1}^{n}(\hat{y}^i-(wx^i+b))$$

最优化

$$f^* = arg \underset{f}{\min} L(f)$$ $$w^*,b^* = arg \underset{w,b}{\min} L(w,b)$$

• 梯度下降
  针对参数$w$，考虑损失函数 $L(w) $
  • 1.随机选择初始值$w^0$
  • 2.计算$\frac{\mathrm{d} L}{\mathrm{d} w}|_{w=w^0}$
  • 3.更新$w_1\leftarrow w_0-\eta \frac{\mathrm{d} L}{\mathrm{d} w}|_{w=w^0}$
    
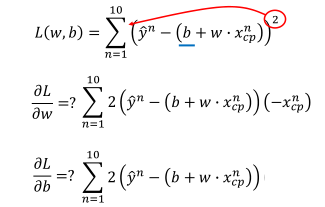
• 存在问题：
  • 驻点
  • 局部最小值

    模型选择

• 过拟合问题
  
  

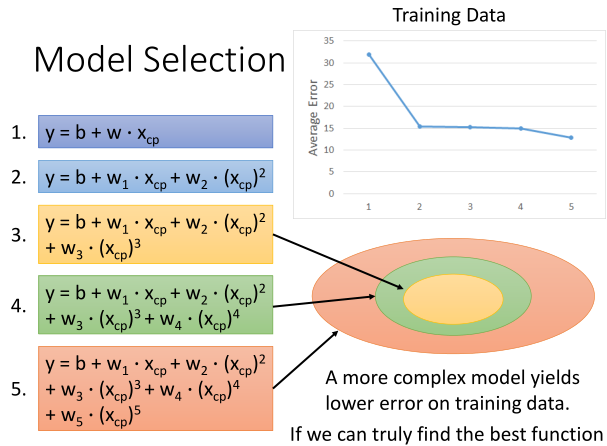
  • 这5个模型都是线性模型（是否线性模型看w的次数）
  • 更复杂的模型具有更小的训练误差
  • 更复杂的模型不一定具有更小的泛化误差（发生过拟合）

• 正则化

  • $ L(w,b) = \sum_{n}(\hat{y}^n-(b+\sum w_ix_i))^2 + \lambda \sum(w_i)^2$
  • 更小的$w_i$值代表模型更平滑（考虑下面方程，当$x$变化$\delta x$时，$y$变化为$\sum w_i \delta x_i$，当$w$越小时，$y$变化越小） $$y = b + \sum w_i x_i$$ $$y +\sum w_i \delta x_i= b + \sum w_i (x_i+\delta x_i)$$