误差推导[1]
假设我们现在有一组训练样本$x_1,…,x_n$,每一个$y_i$有一个$x_i$与之对应。其中的对应关系用方程$y = f(x)+\epsilon $表示,其中$\epsilon $满足条件$\epsilon \sim N(0,\sigma^2 )$,$\hat{f}$为一个函数估计。则平方误差的偏差方差分解所得的推导如下:
首先,对于任意随机变量 $X$,有
\begin{aligned}\operatorname {Var} [X]=\operatorname {E} [X^{2}]-{\Big (}\operatorname {E} [X]{\Big )}^{2}\end{aligned}
整理可得,
\begin{aligned}\operatorname {E} [X^{2}]=\operatorname {Var} [X]+{\Big (}\operatorname {E} [X]{\Big )}^{2}\end{aligned}
由于$f$是确定的,有
\begin{aligned}\operatorname {E} [f]=f\end{aligned}
因此,在$ y=f+\varepsilon$以及$ \operatorname {E} [\varepsilon ]=0$ 的情况下,可以推出$\operatorname {E} [y]=\operatorname {E} [f+\varepsilon ]=\operatorname {E} [f]=f$。
另外,由于 $ \operatorname {Var} [\varepsilon ]=\sigma ^{2}$,故
\begin{aligned}\operatorname {Var} [y]=\operatorname {E} [(y-\operatorname {E} [y])^{2}]=\operatorname {E} [(y-f)^{2}]=\operatorname {E} [(f+\varepsilon -f)^{2}]=\operatorname {E} [\varepsilon ^{2}]=\operatorname {Var} [\varepsilon ]+{\Big (}\operatorname {E} [\varepsilon ]{\Big )}^{2}=\sigma ^{2}\end{aligned}
最后,因为 $\varepsilon $和 ${\hat {f}} $是独立的,所以有
\begin{aligned}\operatorname {E} {\big [}(y-{\hat {f}})^{2}{\big ]}&=\operatorname {E} {\big [}(f+\varepsilon -{\hat {f}})^{2}{\big ]}\\&=\operatorname {E} {\big [}(f+\varepsilon -{\hat {f}}+\operatorname {E} [{\hat {f}}]-\operatorname {E} [{\hat {f}}])^{2}{\big ]}\\&=\operatorname {E} {\big [}(f-\operatorname {E} [{\hat {f}}])^{2}{\big ]}+\operatorname {E} [\varepsilon ^{2}]+\operatorname {E} {\big [}(\operatorname {E} [{\hat {f}}]-{\hat {f}})^{2}{\big ]}+2\operatorname {E} {\big [}(f-\operatorname {E} [{\hat {f}}])\varepsilon {\big ]}+2\operatorname {E} {\big [}\varepsilon (\operatorname {E} [{\hat {f}}]-{\hat {f}}){\big ]}+2\operatorname {E} {\big [}(\operatorname {E} [{\hat {f}}]-{\hat {f}})(f-\operatorname {E} [{\hat {f}}]){\big ]}\\&=(f-\operatorname {E} [{\hat {f}}])^{2}+\operatorname {E} [\varepsilon ^{2}]+\operatorname {E} {\big [}(\operatorname {E} [{\hat {f}}]-{\hat {f}})^{2}{\big ]}+2(f-\operatorname {E} [{\hat {f}}])\operatorname {E} [\varepsilon ]+2\operatorname {E} [\varepsilon ]\operatorname {E} {\big [}\operatorname {E} [{\hat {f}}]-{\hat {f}}{\big ]}+2\operatorname {E} {\big [}\operatorname {E} [{\hat {f}}]-{\hat {f}}{\big ]}(f-\operatorname {E} [{\hat {f}}])\\&=(f-\operatorname {E} [{\hat {f}}])^{2}+\operatorname {E} [\varepsilon ^{2}]+\operatorname {E} {\big [}(\operatorname {E} [{\hat {f}}]-{\hat {f}})^{2}{\big ]}\\&=(f-\operatorname {E} [{\hat {f}}])^{2}+\operatorname {Var} [y]+\operatorname {Var} {\big [}{\hat {f}}{\big ]}\\&=\operatorname {Bias} [{\hat {f}}]^{2}+\operatorname {Var} [y]+\operatorname {Var} {\big [}{\hat {f}}{\big ]}\\&=\operatorname {Bias} [{\hat {f}}]^{2}+\sigma ^{2}+\operatorname {Var} {\big [}{\hat {f}}{\big ]}\\\end{aligned}
Bias v.s. Variance
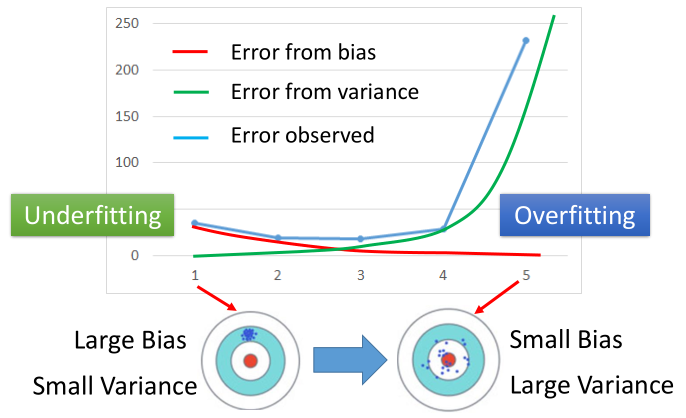
- 简单模型,具有较大的bias,但是variance较小
- 复杂模型,具有较小的bias,但是variance较大
bias太大怎么办?
- 判断方法
- 如果模型无法拟合训练样本,那么bias就会很大——欠拟合
- 如果模型能够很好地拟合训练样本,但是测试误差很大,那么模型就有很大的variance——过拟合
- 针对bias问题,需要重新设计模型:
- 添加新的特征
- 使用更加复杂的模型
variance太大怎么办?
- 收集更多训练样本
- 正则化
=>可能导致bias增大
模型选择[2]
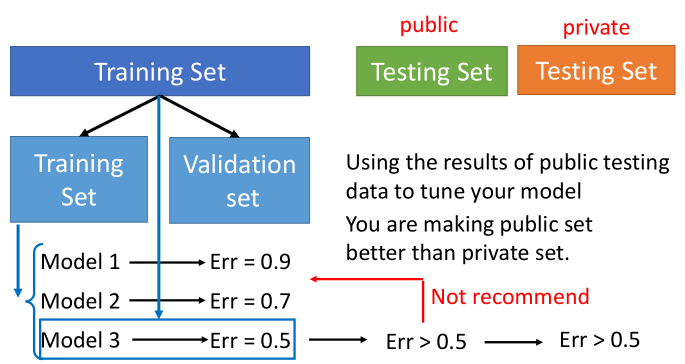
1.总是使用交叉验证,而非使用单一的验证集。
2.相信交叉验证分数,而非排行榜分数。
3.最终模型选择2个得分最高且差异最大的模型。
- 交叉验证
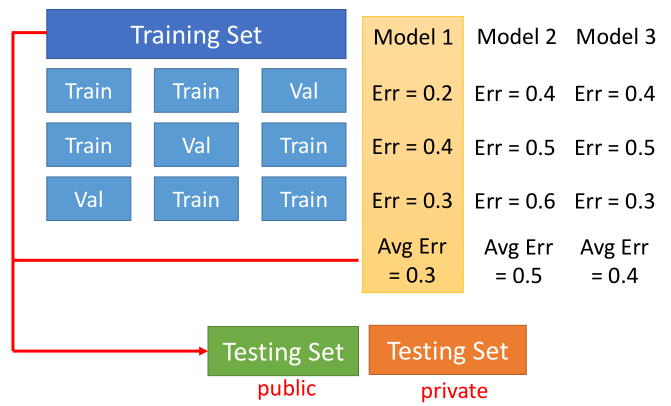
- N折交叉验证
引用
[1].https://en.wikipedia.org/wiki/Bias%E2%80%93variance_tradeoff
[2].http://www.chioka.in/how-to-select-your-final-models-in-a-kaggle-competitio/
